What is Law of Rational Indices?
Law of Rational Indices
The law of rational indices was deduced by Hauy.
The law of rational indices states that the intercepts of any face of a crystal along the crystallographic axes are either equal to the unit intercepts or some simple whole number multiples of them.
The faces of crystals and also planes within crystals can be characterized by means of a suitable set of coordinates.
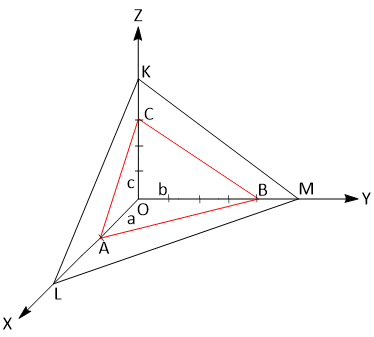
Let consider the three axes OX, OY, OZ which are cut by a crystal face ABC at distances OA, OB, and OC from the origin. Let OX, OY, and OZ represent the three crystallographic axes and let ABC be a unit plane. The unit intercepts will then be a, b and c.
According to the above law, the intercepts of any face such as KLM, on the same three Axes will be simple whole number multiples of a,b and c respectively. These distances are called intercepts. It is found that if the axes are suitably chosen, the intercepts of different faces upon them bear a simple ratio to each other or a given face may cut an axis at infinity. This is called the law of rational intercepts or indices.
