Parachor:
Macleod in 1923 gave the following relation between the surface tension (γ) and density (D) for a normal liquid-
C=γ1/4/(D −d)
where d is vapour density of the liquid at given temperature and C is constant.
In 1924, Sugden modified the above equation as-
γ1/4/(D −d)=MC=P
where M is the molecular weight of the liquid and P is the parachor.
At ordinary temperature, d is very small in comparision to D then-
M γ1/4/D=P
If γ=1 at a particular temperature, then-
M/D=P
Thus, at a particular temperature, the molar volume of a liquid having surface tension unity is called Parachor.
If two liquids having the same surface tension are taken whose molecular weights are M1 and M2 and their densities are D1 and D2 respectively, then-
M1 γ1/4/D1=P1
and
M2 γ1/4/D2=P2
P1/P2=(M1/D1)/ (M2/D2)
So, the ratio of parachors of two liquids having the same surface tension is equal to the ratio of molar volumes. Parachor is both an additive and constitutive property.
Parachor Value of some Elements and Groups:
| Element | P Value | Group | P Value |
|---|---|---|---|
| C | 8.6 | C=O | 44.4 |
| H | 15.7 | OH | 30.2 |
| N | 12.5 | COOH | 73.7 |
| O | 19.8 | NO2 | 73.8 |
| Cl | 55.2 | Double Bond | 19.9 |
| Br | 68.8 | Triple Bond | 40.6 |
| I | 90.3 | Six Membered Ring | 1.4 |
Application of Parachor:
Parachor data are used to determine the structure of molecules and the nature of bonds.
Example:
Two structure proposed for QUINONE-
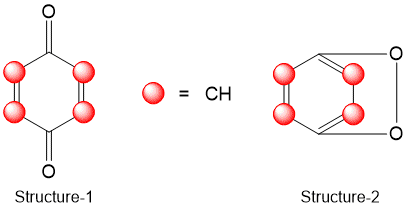
Structure-1
6C=6 X 8.6=51.6
4H=4 X 15.7=62.8
2O=2 X 19.8=39.6
Four double bonds=4 X 19.9=79.6
one 6 membered ring=1 X 1.4=1.4
So, Calculated Parachor=235
Structure-2
6C=6 X 8.6=51.6
4H=4 X 15.7=62.8
2O=2 X 19.8=39.6
Three double bonds=3 X 19.9=59.7
Two 6 membered ring=2 X 1.4=2.8
So, Calculated Parachor=216.5
Since the experimental Parachor is 236.8. Hence structure-1 is correct for QUINONE.
