Beer Lambert Law: Derivation, Application, Limitations, Deviation and Transmittance
Absorption Law
There are two laws which govern the absorption of light by the molecules.
1. Beer's Law
2. Lambert's Law
Beer's Law
The absorbance is directly proportional to the molar concentration of solution.
A ∝ C
Lambert's Law
The absorbance is directly proportinal to the optical path length.A ∝ x
on combining these two laws we get-
A ∝ C x
A = εCx
Absorbance
Absorbance is the maximum capacity of a substance to absorb light of any specified wavelength. Absorbance is equal to the logarithm of the reciprocal of transmittance. Absorbance is expressed as-
A = −log10T
Transmittance: Transmittance is the ratio of reflected light to incident light on an object. Transmittance is expressed as-
T = I/I0
Beer lambert law
Beer-Lambert law defines the relationship between the concentration of a solution and the amount of light absorbed by the solution.
A = εCx
Where-
A = Absorbance
ε = Molar absorptivity (L/mol/cm)
x = Path length of the cuvette containing the sample (cm)
C = Concentration of the compound in the solution (mol/L)
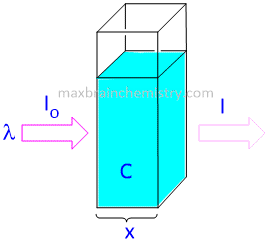
When a beam of monochromatic light is passed through a homogeneous absorbing medium, then the rate of decrease in intensity of radiation with the thickness of absorbing medium is directly proportional to intensity of incident radiation as well as to the concentration of the solution.
Derivation of Beer lambert law
-dI/dx ∝ IC
or, -dI/dx = KIC -----Equation-1
where I=Intensitiy of light at any thickness x
C= concentration of solution
dI=Infinitesimally small decrease in intensity of radiation on passing through infinitesimally small thickness dx of the medium.
dx= infinitesimally small decrease in thickness x
-dI/dx = Rate of decreaseof intensity of radiation with thickness of the absorbing medium.
K= proportionality constant called molar coefficient whose value depends upon the nature of absorbing medium.
On rearrangement of Equation-1, we get-
-dI/I = KCdx -----Equation-2
If Io is the intensity of incident radiation when x = 0, then the intensity of radiation after passing through any finite thickness x of the medium can be obtained by integrating the above equation.
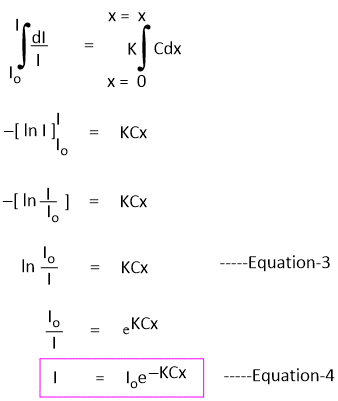
Equation-4 shows that the intensity of a monochromatic beam of light decreases exponentially when the thickness of the medium and intensity increase.
Equation-3 can also be written by changing natural logarithm to the base 10 as -
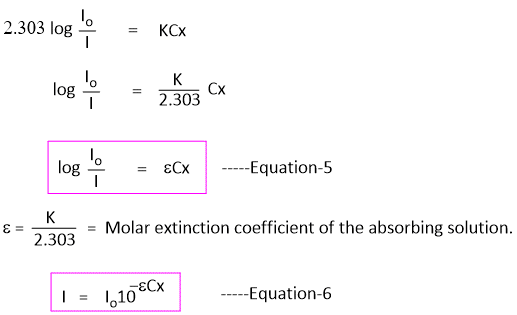
In Equation-5, the term log(Io/I) is called absorbance(A) and is obtained from Lambert Beer's law.
log(Io/I) = A -----Equation-8
Absorbance is a unitless number because Io/I is unitless that depends on the path length, the concentration of absorbing substance, and the wavelength of light.
So, A = εCx -----Equation-9
When C= 1moldm-3 and x = 1cm then-
A = ε -----Equation-10
Hence, the molar extinction coefficient(ε) can be defined as absorbance for a concentration of 1mol.dm-3 and a path length of 1cm.
From Equation-8 and Equation-9 we have-
ε = (log Io/I)/Cx -----Equation-11
The molar extinction coefficient is expressed in liter/mol/cm.
From Equation-8 we have-
A = log(Io/I)
or, A = −log(I/Io)
or, A = log(1/T)
where, I/Io = T = Transmittance and is the ratio of intensity of transmitted light to intensity of light absorbed by solution.
or, A = −logT
Hence, the absorbance is equal to the negative logarithm of transmittance.
T % = (I / I0) x 100 %
we know that, A = log(1/T)
or, A = log(100/T[%])
or, A = 2 − logT[%]
Note:
1. 0% transmittance means total absorption (i.e. I = 0)
2. 50% transmittance means half the light is transmitted (i.e. I = 50% of I0)
3. 100% transmittance means no absorption (total light is transmitted i.e. I = I0)
Thus, the greater the amount of light absorbed by the sample, the smaller the percent transmittance.
Applications of Transmittance
The measurement of transmittance has many applications, some of which are given below-
1. Measuring concentrations of chemicals in solutions
2. Water clarity
3. Grade of syrup
4. Testing window tint films and glass clarity
5. Atmospheric haze
Application of Beer Lambert's law
Applications of beer lambert law are given below-
1. The concentration of the unknown solution can be determined by comparison with a solution of known concentration using a spectrophotometer, the principle is based on Beer-Lambert Law.
2. The purity of a substance can be checked by the measurement of the absorbance of a compound by using a spectrophotometer.
3. Beer Lambert law is used to describe solar or stellar radiation in the atmosphere.
Limitations of Beer Lambert's law
The limitations of Beer-lambert law are given below-
1. Beer-Lambert law is only valid on monochromatic light.
2. This law is applicable under a low concentration range where interactions between molecules are not considered.
3. This law is also invalid when radiations of very high intensities are used.
Deviation of Beer Lambert's law
The Beer-Lambert's law maintains linearity under specific conditions only. When a plot of absorbance as a function of concentration at a particular path and wavelength of monochromatic is drawn, a straight line passing through the origin is obtained. But when concentration is very high, a plot of absorbance and concentration deviates from linear behavior.
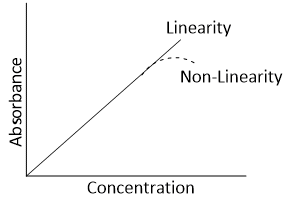
The main causes of such deviation from Beer Lambert’s law are given below-
1. The deviation may occur when the light of a single wavelength is not used.
2. Polymerization of solutes during the measurements.
3. Association, dissociation, or ionization of solutes causes deviation.
4. Presence of some other substance that absorbs at the same wavelength as the solute may cause deviation.
5. The presence of some impurities in the colored compounds may cause deviation.
What is the concentration of a solution whose absorbance is 0.21 when placed in a tube of path length 10cm (λmax = 245nm and εmax = 31500M/cm)
Hints: C = A/εl
0.21/(31500 x 10) = 6.67 x 10−7M
%transmittance of a transition metal complex at 360nm at 25°C is 25% for a 6 x 10−4mol/ltr solution in a 1cm cell. What will be the molar absorption coefficiebt in the unit of L mol−1 cm−1?
Hints: A = 2 − log(%T)
A = 2 − log 25
A = 2 − 2log 5
A = 2 − 2 x 0.6990
A = 0.6
Now, ε = A/Cx
ε = 0.6/(6 x 10−4 x 1)
ε = 1 x 103L mol−1 cm−1
Rupa prepared a calibration curve by measuring of the absorbance of five standard solutions of a compound at 300nm. A cuvette with a path length of 5cm was used in the stratosphere the slope if the curve was 300 L/mol the molar absorptivity of the compound will be?
Hints: Slope = 300L/mol
Path Length = 5cm
Molar Absorptivity = ?
Slope = Molar Absorptivity x Path Length
300 = Molar Absorptivity x 5
Molar Absorptivity = 60Lmol−1cm−1
In a spectrophotometric cell of 2.0 cm path length, the solution of a substance shows the absorbance value of 1.0. If the molar absorptivity of the compound is 2 x 104L mol−1cm−1, calculate the concentration of the substance in solution. What is the concentration of the substance in that solution?
Hints: A = ε C L
Path Length (L) = 2.0cm
Molar Absorptivity (ε) = 2 x 104L mol−1cm−1
Absorbance (A) = 1.0
1 = 2 x 104 x C x 2
C = 2.5 x 10-5
