Wave Function for sp, sp2 and sp3 Hybrid Orbitals
The wave function of hybrid orbitals are obtained by the linear combination of the angular wave functions of the appropriate atomic orbitals.
1. Ψ1 = a1Ψs + b1Ψ2p ---Equation-1
2. Ψ2 = a2Ψs + b2Ψ2p ---Equation-2
The values of the linear combination coefficients a1, b1, a2 and b2 may be determined by the following considerations-
I. Ψ1 and Ψ2 are normalized
II. Ψ1 and Ψ2 are orthogonal
III. Ψ1 and Ψ2 are equivalent
From Condition-1: Ψ1 and Ψ2 are normalized
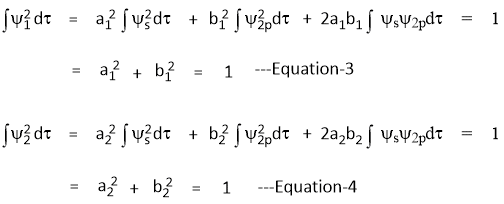
From Condition-2: Ψ1 and Ψ2 are orthogonal
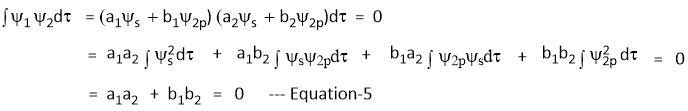
Sine the s-orbital is sperically symmetrical and the two hybrid orbitals Ψ1 and Ψ2 are equivalent, the share of 's' function is equal in both Ψ1 and Ψ2
i.e.

Ψsp2(1) = a1Ψ2s + b1Ψ2px + c1Ψ2py ---Equation-1
Ψsp2(2) = a2Ψ2s + b2Ψ2px + c2Ψ2py ---Equation-2
Ψsp2(3) = a3Ψ2s + b3Ψ2px + c3Ψ2py ---Equation-3
Since, s orbital is equally distributed among the three hubrid orbitals, so, we have-
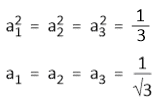
Assume that Ψsp2(1) points towards the x-axis. Hence, this hybrid orbital will have contribution from 2s and 2px orbitals only. The contribution of the 2py orbital will be zero. So, c1 = 0.
Since, Ψsp2(1) is normalized,
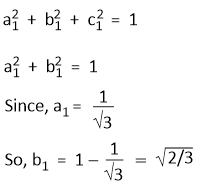
Since, Ψsp2(1) and Ψsp2(2) are orthogonal and Ψsp2(1) and Ψsp2(3) are also orthogonal. Hence-
a1a2 + b1b2 = 0
a1a3 + b1b3 = 0
Hence,
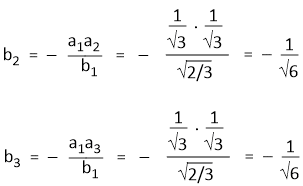
Again, Since Ψsp2(2) is normalized-
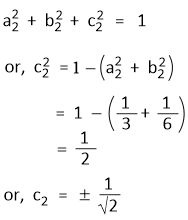
Further, Ψsp2(3) is also normalized-
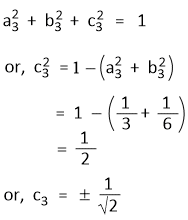
Let c2 have a positive value, then the value of c3 will have to be negative as Ψsp2(2) and Ψsp2(3) are orthogonal.
i.e. a2a3 + b2b3 + c2c3 = 0
Thus, If, c2 = +1/√2 and c3 = −1/√2
Hence, the three wave functions are-
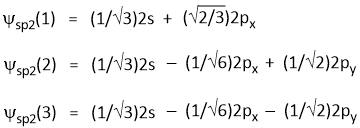
Ψsp3(1) = a1Ψ2s + b1Ψ2px + c1Ψ2py + d1Ψ2pz ---Equation-1
Ψsp3(2) = a2Ψ2s + b2Ψ2px + c2Ψ2py + d2Ψ2pz ---Equation-2
Ψsp3(3) = a1Ψ2s + b3Ψ2px + c3Ψ2py + d3Ψ2pz ---Equation-3
Ψsp3(4) = a4Ψ2s + b4Ψ2px + c4Ψ2py + d4Ψ2pz ---Equation-4
Since the s orbital is equally distributed among the four hybrid orbitals. So, we have-
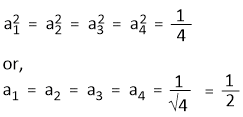
Assuming that Ψsp3(1) is developed along x-axis, so the contribution from 2py and 2pz orbitals to the hybrid orbitals is zero.
that means, c1 = d1 = 0
Since, Ψsp3(1) is normalized.
Hence,
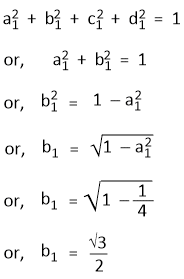
The orthogonality conditions for Ψsp3(1) and Ψsp3(2), Ψsp3(1) and Ψsp3(3) and Ψsp3(1) and Ψsp3(4) are -
a1a2 + b1b2 = 0
or, b2 = − a1a2/b1
or, b2 = − 1/2√3
a1a3 + b1b3 = 0
b3 = − a1a3/b1
or, b3 = − 1/2√3
a1a4 + b1b4 = 0
b4 = − a1a4/b1
or, b4 = − 1/2√3
Assuming that Ψsp3(2) lies in the xz-plane, the hybrid orbital will have contributions from 2s, 2px and 2pz orbitals and the contribution of 2py to Ψsp3(2) is zero.
That means,
c2 = 0
The normalized condition for Ψsp3(2) gives-
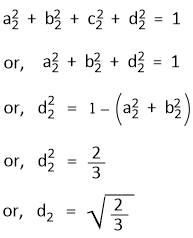
The requirement of orthogonality conditions for Ψsp3(2) and Ψsp3(3), and for Ψsp3(2) and Ψsp3(4) gives-
a2a3 + b2b3 + d2d3 = 0
or, d3 = −(a2a3 + b2b3)/d2
or, d3 = − 1/√6
and a2a4 + b2b4 + d2d4 = 0
or, d4 = −(a2a4 + b2b4)/d2
or, d4 = − 1/√6
The normalization required for Ψsp3(3) gives-
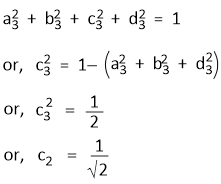
Similarly, normalization requirement for Ψsp3(4) and the orthogonality condition between Ψsp3(3) and Ψsp3(4) gives-
c4 = − 1/√4
Hence, the four sp3 hybrid orbital wave functions can be written as-
Ψsp3(1) = (1/2)Ψ2s + (√3/2)Ψ2p
Ψsp3(2) = (1/2)Ψ2s − (1/2)Ψ2px + (√2/√3)Ψ2py
Ψsp3(3) = (1/2)Ψ2s − (1/2√3)Ψ2px + (1/√2)Ψ2py − (1/√6)Ψ2pz
Ψsp3(4) = (1/2)Ψ2s − (1/2√3)Ψ2px + (1/√2)Ψ2py − (1/√6)Ψ2pz
sp Hybrid Orbital Wave Function
The combination of one s and one 2p orbital, giving two hybrid orbitals may be expressed as-1. Ψ1 = a1Ψs + b1Ψ2p ---Equation-1
2. Ψ2 = a2Ψs + b2Ψ2p ---Equation-2
The values of the linear combination coefficients a1, b1, a2 and b2 may be determined by the following considerations-
I. Ψ1 and Ψ2 are normalized
II. Ψ1 and Ψ2 are orthogonal
III. Ψ1 and Ψ2 are equivalent
From Condition-1: Ψ1 and Ψ2 are normalized
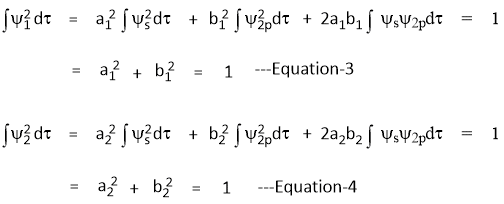
From Condition-2: Ψ1 and Ψ2 are orthogonal
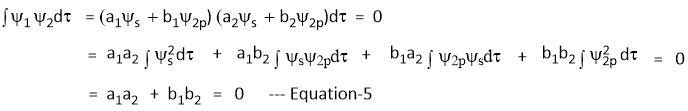
Sine the s-orbital is sperically symmetrical and the two hybrid orbitals Ψ1 and Ψ2 are equivalent, the share of 's' function is equal in both Ψ1 and Ψ2
i.e.

sp2 Hybrid Orbital Wave Function
Wave functions for three hybrid orbitals may be written as-Ψsp2(1) = a1Ψ2s + b1Ψ2px + c1Ψ2py ---Equation-1
Ψsp2(2) = a2Ψ2s + b2Ψ2px + c2Ψ2py ---Equation-2
Ψsp2(3) = a3Ψ2s + b3Ψ2px + c3Ψ2py ---Equation-3
Since, s orbital is equally distributed among the three hubrid orbitals, so, we have-
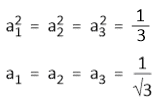
Assume that Ψsp2(1) points towards the x-axis. Hence, this hybrid orbital will have contribution from 2s and 2px orbitals only. The contribution of the 2py orbital will be zero. So, c1 = 0.
Since, Ψsp2(1) is normalized,
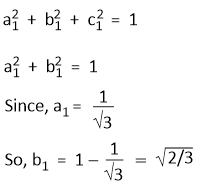
Since, Ψsp2(1) and Ψsp2(2) are orthogonal and Ψsp2(1) and Ψsp2(3) are also orthogonal. Hence-
a1a2 + b1b2 = 0
a1a3 + b1b3 = 0
Hence,
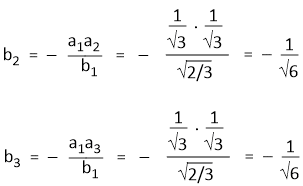
Again, Since Ψsp2(2) is normalized-
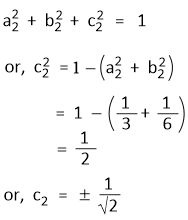
Further, Ψsp2(3) is also normalized-
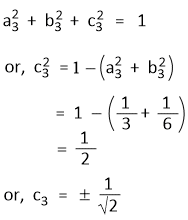
Let c2 have a positive value, then the value of c3 will have to be negative as Ψsp2(2) and Ψsp2(3) are orthogonal.
i.e. a2a3 + b2b3 + c2c3 = 0
Thus, If, c2 = +1/√2 and c3 = −1/√2
Hence, the three wave functions are-
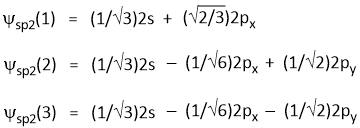
sp3 Hybrid Orbital Wave Function
The wave function of four sp3 hybrid orbitals may be written as-Ψsp3(1) = a1Ψ2s + b1Ψ2px + c1Ψ2py + d1Ψ2pz ---Equation-1
Ψsp3(2) = a2Ψ2s + b2Ψ2px + c2Ψ2py + d2Ψ2pz ---Equation-2
Ψsp3(3) = a1Ψ2s + b3Ψ2px + c3Ψ2py + d3Ψ2pz ---Equation-3
Ψsp3(4) = a4Ψ2s + b4Ψ2px + c4Ψ2py + d4Ψ2pz ---Equation-4
Since the s orbital is equally distributed among the four hybrid orbitals. So, we have-
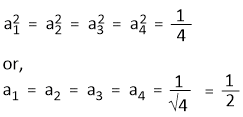
Assuming that Ψsp3(1) is developed along x-axis, so the contribution from 2py and 2pz orbitals to the hybrid orbitals is zero.
that means, c1 = d1 = 0
Since, Ψsp3(1) is normalized.
Hence,
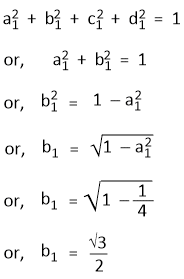
The orthogonality conditions for Ψsp3(1) and Ψsp3(2), Ψsp3(1) and Ψsp3(3) and Ψsp3(1) and Ψsp3(4) are -
a1a2 + b1b2 = 0
or, b2 = − a1a2/b1
or, b2 = − 1/2√3
a1a3 + b1b3 = 0
b3 = − a1a3/b1
or, b3 = − 1/2√3
a1a4 + b1b4 = 0
b4 = − a1a4/b1
or, b4 = − 1/2√3
Assuming that Ψsp3(2) lies in the xz-plane, the hybrid orbital will have contributions from 2s, 2px and 2pz orbitals and the contribution of 2py to Ψsp3(2) is zero.
That means,
c2 = 0
The normalized condition for Ψsp3(2) gives-
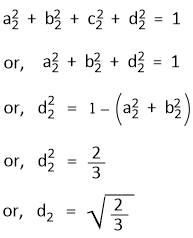
The requirement of orthogonality conditions for Ψsp3(2) and Ψsp3(3), and for Ψsp3(2) and Ψsp3(4) gives-
a2a3 + b2b3 + d2d3 = 0
or, d3 = −(a2a3 + b2b3)/d2
or, d3 = − 1/√6
and a2a4 + b2b4 + d2d4 = 0
or, d4 = −(a2a4 + b2b4)/d2
or, d4 = − 1/√6
The normalization required for Ψsp3(3) gives-
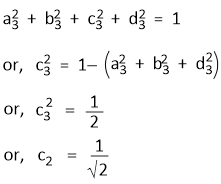
Similarly, normalization requirement for Ψsp3(4) and the orthogonality condition between Ψsp3(3) and Ψsp3(4) gives-
c4 = − 1/√4
Hence, the four sp3 hybrid orbital wave functions can be written as-
Ψsp3(1) = (1/2)Ψ2s + (√3/2)Ψ2p
Ψsp3(2) = (1/2)Ψ2s − (1/2)Ψ2px + (√2/√3)Ψ2py
Ψsp3(3) = (1/2)Ψ2s − (1/2√3)Ψ2px + (1/√2)Ψ2py − (1/√6)Ψ2pz
Ψsp3(4) = (1/2)Ψ2s − (1/2√3)Ψ2px + (1/√2)Ψ2py − (1/√6)Ψ2pz
Share
