Measurement of Transference Number by Moving Boundary Method
Measurement of Transport Number by Moving Boundary Method
The moving boundary method is based on the direct observation of migration of ions under the influence of applied potential. This method is very accurate and has been used in recent years for precision measurements. The apparatus used consists of a long vertical tube fitted with two electrodes at the two ends as shown in Figure.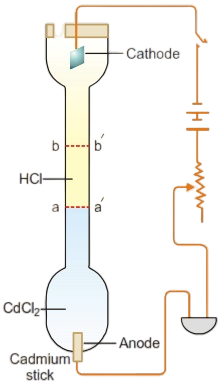
The tube is filled with a solution of cadmium chloride (CdCl2) at the lower end and hydrochloric acid at the upper end in a way that there is a sharp boundary between the two (due to difference in their refractive indices).
The platinum cathode dipped in HCl solution is inserted at the top and the anode (cadmium stick) is introduced at the bottom. On passing electric current through the apparatus, hydrogen gas is evolved at the cathode and H+ ions move toward the anode. The H+ ions are replaced by Cd+2 ions and hence the boundary line moves in the upward direction. By noting the length through which the boundary moves and the quantity of electricity passed through the cell, the transport number of H+ ion can be calculated.
In general, if the transport number of a cation A+ is to be determined, the electrolyte AX solution is taken in the upper part of the apparatus and a layer of another electrolyte BX having the common ion X– is introduced in the lower part of the apparatus. The electrolyte BX is selected so that the velocity of B+ ion is less than that of A+ ion. The situation is shown in Figure
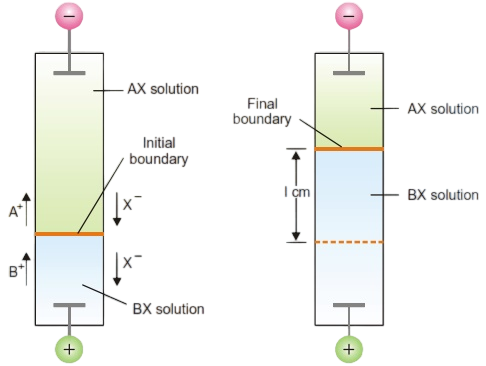
Calculation of Transference Number by Moving Boundary Method
Let c be the original concentration of A+ ions in gram-equivalents per ml of the solution.If the distance through which boundary moves = l cm, and the area of cross-section of the tube = s sq cm.
Then the number of equivalents of A+ moving upward = s × l × c
Let the number of Faradays of current passed = n
The fraction of current carried by A+ ions = n x tA+
Hence, n x tA+ = s × l × c
and tA+ = (s × l × c) / n -----Equation-1
where n = Q/F. Q being the quantity of current passed and F stands for Faraday (= 96, 500 coulombs).
The above expression can now be written as-
tA+ = (s × l × c x F) / Q -----Equation-2
With the help of the equation-1 and 2, the value of tA+ (transport number of A+), can be found from the experimental values of s, l, c and n.
[Source:Essentials of Physical Chemistry; Arun Bahl, B. S. Bahl & G. D. Tuli]
