Bragg's Equation

When a beam of light falls on a crystal plane composed of regularly arranged particles, the X- rays are diffracted. If the waves are in phase after reflection,the difference in distance travelled by the two rays must be eqaul to an integral number of wavelength, nλ for constructive interference.
                     
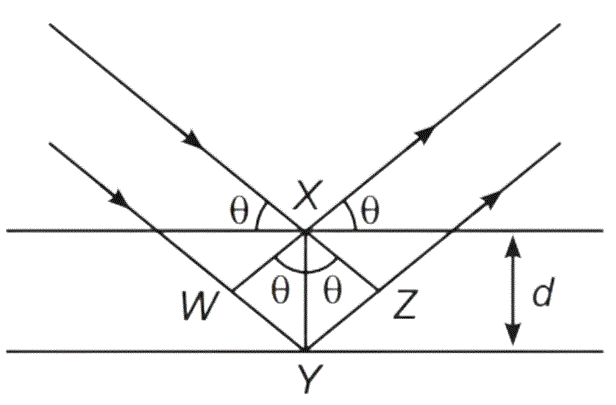
Thus, Path difference = WY + YZ
       = XY sinθ + XY sinθ
       = 2XY sinθ
       = 2d sinθ
       So, nλ = 2d sinθ
This equation is Known as Bragg's equation.
       where, n = 1,2,3...(diffrection order)
       λ = wavelength of X-rays
       d = distance between planes
       θ = angle at which interference occurs.

How to Utilize Bragg's Equation to Determine Crystal Structure

The X-ray diffraction processes used for crystals are of two types-the rotating crystal process and powder process. In the latter, a powdered sample is used in place of crystal and hence simple exposure of X-rays is sufficient and so no rotation is necessary because powdered sample has crystals arranged in all possible orientations.
In rotating crystal process, a narrow beam of X-ray strikes a crystal mounted on the turn table. The crystal is rotated so as to increase glancing angle at which the X-rays are incident at the exposed face of the crystal. The intensities of the reflected rays are measured on the recording device. The angle of the maximum reflections is θ of Bragg's equation. The process is repeated for each face of the crystal. The lowest angle at which the maximum deflection occurs corresponds to n = 1, called Ist order reflection and so on. Generally, the angle of 1st order reflection is taken as θ in order to set the n value equal to 1.


If the θ value of the Ist order reflection from three faces viz., 100, 111 & 112 of NaCl crystal be 5.9°, 8.4° and 5.2° respectively; then from Bragg's equation, we get-
d = (nλ/2)sin⁻¹θ
As n and λ are the same in each case,
Hence, d ∝ sin⁻¹θ
or, d ∝ 1/sinθ
Therefore, d value in three faces are in the ratio-
d₁₀₀ : d₁₁₁: d₁₁₂ = (1/sin 5.9) : (1/sin 8.4) : (1/sin 5.2)
or, d₁₀₀ : d₁₁₁: d₁₁₂ = (1/0.103) : (1/0.146) : (1/0.091)
or, d₁₀₀ : d₁₁₁: d₁₁₂ = 1.000 : 0.704 : 1.154
The ratio is closer to that exists in FCC. Hence, NaCl lattice has FCC structure of Na⁺ ions interlocked with similar pattern of Cl⁻ions.

Bragg's Law Calculator

Order of Diffraction (n): Wavelength (λ in nm): Interplanar Spacing (d in nm):

 Share